Song Pong
Synchronizing pong to music with constrained optimization
Lately I’ve been experimenting with music visualizers. One of my favorites is inspired by the classic arcade game pong. In classic pong a ball bounces off of paddles in a steady rhythm. What if we synchronize the bounces to the beat of a song, making the paddles dance?
To make this possible we alter the physics of the game so that the ball moves at a constant speed, and paddles can move anywhere on their respective halves of the screen.
We also retain these rules from the classic game:
The contact point of the ball on the paddle determines its angle of reflection
Paddles have no speed limit
The ball bounces off the top and bottom of the screen
These physics give us the necessary degrees of freedom to move the paddles to hit the ball at any desired times.
One simple strategy to satisfy any timing requirements is to keep both paddles close to the center. This gives us little horizontal space, but vertical space is effectively infinite since the ball can bounce off the top and bottom edges of the screen. For any desired shot duration, we can slow the horizontal velocity to match it by hitting the ball more vertically. While this argument shows a solution exists for any input, it certainly isn't exciting to watch.
What makes a visualization appealing, though? One desirable property is the utilization of screen space; a game stuck in a small region feels cramped and underwhelming. Closely related is dynamism of movement; spectators enjoy watching players make heroic efforts to hit a ball just within reach.
Unfortunately it's difficult to write an algorithm to maximize screen usage while guaranteeing a valid game. If a paddle hits the ball far from the screen's center, the ball may not have time to cross the screen for the next beat. Any movement of the paddles must account for the potential impact on future moves. This is the crux of the problem: while respecting the beat of the song and the physics of the game, where should the paddles hit the ball on each beat to maximize screen utilization?
Constrained Optimization
Fortunately there is a mature field dedicated to optimizing an objective (screen utilization) with respect to variables (the locations of bounces) in the presence of constraints on those variables (physics and the beats of the song). If we write our requirements as a constrained optimization problem, we can use an off-the-shelf solver to compute optimal paddle positions instead of designing an algorithm ourselves.
Formulating the task as a constrained optimization problem has several advantages. If we change the physics we simply need to update our constraints, while an algorithm may need to be rewritten. In a similar vein, it lets us easily experiment with objectives. Developing appealing animations is an iterative process, which the declarative style of constrained optimization facilitates.
That sounds great, but modeling 2D constraints is hard; is our game truly two-dimensional? It turns out modeling only the horizontal component is sufficient! In our ruleset, the ball moves at a constant speed, so its vertical velocity is exactly determined by its horizontal velocity. By simulating the game we can compute the ball's vertical position at any time.
Knowing the ball's vertical position also gives us the vertical position of the paddles since it must match the ball's position to hit it (plus a small delta to achieve the desired angle). Between hits, we simply linearly interpolate positions to achieve smooth movement. Thus we only need our solver to compute the horizontal positions and velocities at the times when the paddles hit the ball; the rest follows from the physics of the game.
Constants
Let's start by defining the hardcoded parameters of the game:
Timing inputs
Next we have the beat times we’d like to synchronize. Each t represents the time when the ball should hit a paddle. We obtain these times from MIDI files, though in the future I’d like to explore more automated ways of extracting them from audio.
We take the differences between adjacent times to get the duration the ball should travel each shot. Each d represents the time interval between two consecutive hits of the ball.
These are all the fixed inputs we provide to the solver. Now we’ll define the variables we’d like to optimize and their relationships to other quantities.
Variables
Remember we only need to optimize horizontal positions and velocities.
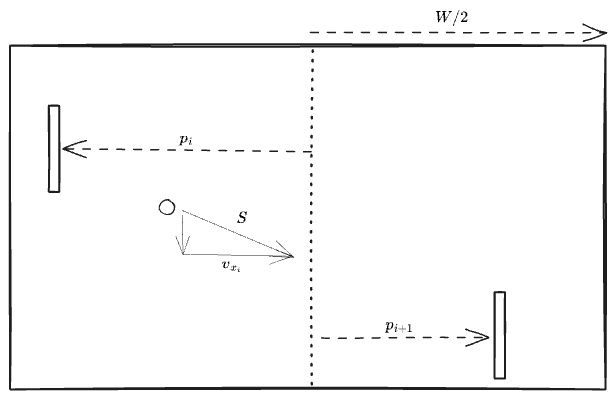
Each p_i represents the horizontal distance of the paddle from the center when it hits the ball for the i-th time. Even indices (p_0, p_2, …) represent the left paddle, while odd indices (p_1, p_3, …) represent the right paddle.
The set of ball horizontal velocities. Each v_i represents the horizontal velocity of the ball after the i-th hit. To make it easier to construct constraints, we define these to always be positive no matter if the ball is moving left or right.
Constraints
First we constrain paddles to stay on their respective halves of the screen:
We defined p as the distance from the center so it’s nonnegative no matter which side of the screen it’s on.
Next we constrain the magnitude of the ball's horizontal velocity to be positive and not exceeding its total speed S.
These two constraints fully define the physics of our game. We add one final constraint to enforce beat synchronization:
This ensures that the ball reaches the next paddle at the correct time. The left hand side represents the total horizontal distance traveled (sum of distances from center for two consecutive paddle hits), which must equal the product of the duration of the shot and the ball's horizontal velocity.
Objective
We know there is a degenerate solution in which the paddles are stuck in the center. A natural thought is to encourage the opposite; maximize the distance from the center.
Our objective, then, is to maximize the sum of the paddle’s distances from the center.
Solving the Problem
With our mathematical formulation in hand, all that’s left is to solve it. All of our constraints are linear, so any linear programming (LP) solver will suffice. I chose CVXPY for its simplicity and generality. CVXPY solves convex optimization problems, of which LP problems are a subset. While we don’t require its full feature set for this task, the flexibility to support more complex objectives and constraints facilitates creative exploration.
With CVXPY, we can express the constraints enumerated above as follows:
Sure enough, the code closely matches the formulas. I actually find the code easier to follow than the formulas due to the descriptive variable names.
The solver returns the horizontal positions where the paddles should hit the ball as well as the horizontal velocities of the ball, from which we can easily compute the angles of reflection. This is enough to compute the vertical positions via simulation.
To animate the final result, we use the positions of the ball and paddles at the time of each hit as keyframes. Between hits we interpolate the positions to create a smooth animation.
Conclusion
Visualization is an extremely open-ended problem, and ultimately the only judges are our own eyes. More often than not the results depend on which algorithms we know. I suspect there are many more visualizers powered by constrained optimization waiting to be discovered; I’d love to hear about them!
The code is open source: Github Repo
Acknowledgements
Thanks to Pat O’Neill for reading drafts of this post.



Very cool! You could also possibly constrain the problem even further so that the hight of the paddle when hitting the ball is proportional to the note pitch. In that case, and if using a single instrument, the resulting video would be an encoding of the song.